提示: 关于 RNN 的内容将横跨好几篇文章,包括基本的 RNN 结构、支持字符级序列生成的纯 TensorFlow 实现等等。而关于 RNN 的后续文章会包含更多高级主题,比如更加复杂的用于机器翻译任务的 Attention 机制等。
一、概述 使用循环结构拥有很多优势,最突出的一个优势就是它们能够在内存中存储前一个输入的表示。如此,我们就可以更好的预测后续的输出内容。持续追踪内存中的长数据流会出现很多的问题,比如 BPTT 算法中出现的梯度消失(gradient vanishing)问题就是其中之一。幸运的是,我们可以对架构做出一些改进来解决这个问题。
二、CHAR-RNN 我们不会去专门实现一个纯 TensorFlow 版本的单字符生成模型。相反,现在这个模型的目标是从每个输入句子中以每次一个字母的方式来读取字符流,并预测下一个字母是什么。在训练期间,我们将句子中的字母提供给网络,并用于生成输出的字母。而在推断(生成)期间,我们则会将上一次的输出作为新的输入(使用随机的 token 作为第一个输入)。
对于文本数据来说,我们做了一些预处理,请查看这个 GitHub 仓库来获取更多信息。
输入样例 :Hello there Charlie, how are you? Today I want a nice day. All I want for myself is a car.
DATA_SIZE:输入的长度,即 len(input);
BATCH_SIZE:每批的序列个数;
NUM_STEPS:每个切片的 token 数,即序列的长度 seq_len;
STATE_SIZE:每个隐层状态的隐层节点数,即值 H;
num_batches:数据集小批量化后的批量数
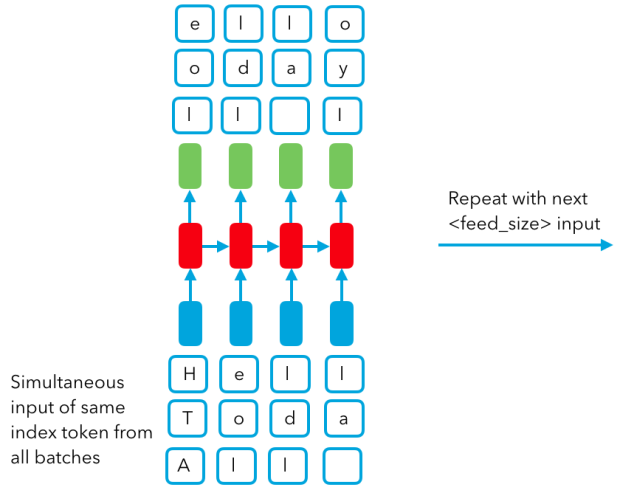
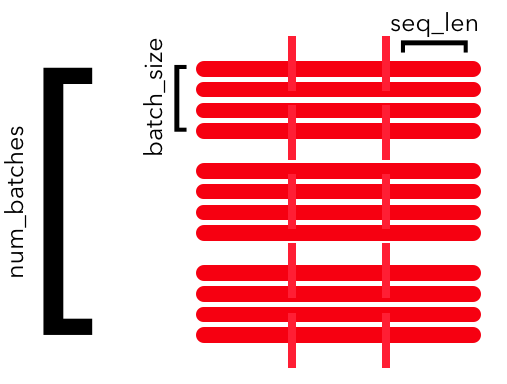
注意: 由于我们是一行一行的将数据输入进 RNN 单元的,因此我们需要一列一列的将数据组成张量输入到网络中去,即我们必须把原始数据进行 reshape 处理。此外,每个字母都将作为一个被嵌入的独热编码(one-hot encoding,译注:又称 1-of-k encoding)的向量输入。在上图中,每个句子数据都被完美的切分进了一组组小批量数据,这只不过是为了达到更好的可视化目的,这样你就可以看到输入是怎样被切分的了。在实际的 -RNN 实现中,我们并不关心一个具体的句子,我们只是将整个输入切分成 num_batches 个批次,每个批次彼此独立,所以每个输入的长度都是 num_steps,即 seq_len。
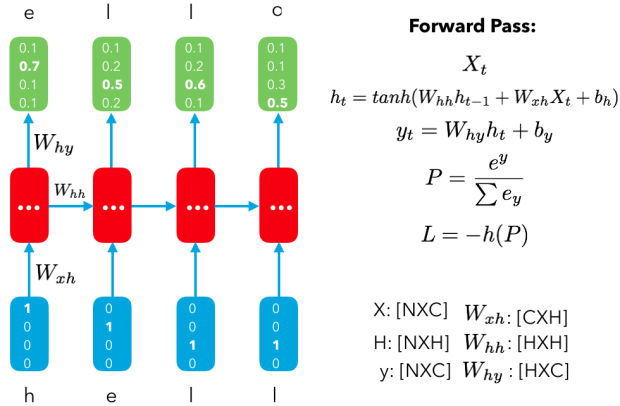
三、反向传播 RNN 版本的反向传播 BPTT 刚开始可能有点混乱,尤其是计算隐藏状态对输入的影响之时。下面的代码使用原生 numpy 实现,符合下图中我的公式推导逻辑。
前向传播:
1 2 3 4 5 6 7 for t in xrange(len(inputs)): xs[t] = np.zeros((vocab_size,1 )) xs[t][inputs[t]] = 1 hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t-1 ]) + bh) ys[t] = np.dot(Why, hs[t]) + by ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) loss += -np.log(ps[t][targets[t],0 ])
反向传播:
1 2 3 4 5 6 7 8 9 10 11 for t in reversed(xrange(len(inputs))): dy = np.copy(ps[t]) dy[targets[t]] -= 1 dWhy += np.dot(dy, hs[t].T) dby += dy dh = np.dot(Why.T, dy) + dhnext dhraw = (1 - hs[t] * hs[t]) * dh dbh += dhraw dWxh += np.dot(dhraw, xs[t].T) dWhh += np.dot(dhraw, hs[t-1 ].T) dhnext = np.dot(Whh.T, dhraw)
张量的形状 在实现之前,我们来谈谈张量的形状。在这个 CHAR-RNN 的例子上讲述张量形状这个概念有点奇怪,因此我会向你解释如何对其进行批量化以及它们是怎样完成 seq2seq 任务的。
这个任务对于一次性输入整行(全部 batch_size 个序列的)seq_len 这点上有点奇怪。通常来说,我们一次只传递一个批量,每个批量都有 batch_size 个序列,所以形状为(batch_size, seq_len)。我们通常也不会用 seq_len 来做分割,而是取整个序列的长度。对于 seq2seq 任务而言,本系列的第 2、3 和 5 篇文章中看到,我们会将大小为 batch_size 一个批量的序列作为输入,其中每个序列的长度为seq_len 。我们不能像在图中那样指定 seq_len,因为实际的seq_len 会根据全部样本的特点填充到最大值。我们会在比最大长度短的所有句子后填充一些填充符,从而达到最大值。不过现在还不是深入讨论这个问题的时候。
四、Char-RNN 的 TensorFlow 实现(无 RNN 抽象) 我们将使用没有 RNN 类抽象的纯 TensorFlow 进行实现。同时还将使用我们自己的权重集来真正理解输入数据的流向以及输出是如何生成的。在这里我们只讨论代码里一些重点部分,而完整的代码我将给出相关链接。如果你想要使用 TF RNN 类进行实现,请转到本文第五小节。
重点:
首先我想讨论下如何生成批量化的数据。你可能注意到了,我们有一个额外的步骤,那就是将数据进行批量化处理,然后再将数据分割进 seq_len。这么做的原因是为了消除 RNN 结构中 BPTT 算法中产生的梯度消失问题。本质上来说,我们并不能同时处理多个字符。这是因为在反向传播中,如果序列太长,梯度就会下降得很快。因此,一个简单的技巧是保存一个 seq_len 长度的输出状态,然后将其作为下一个 seq_len 的 initial_state。这种由我们自行选择(使用 BPTT 来)处理的个数和更新频率的做法,就是所谓的截断反向传播(truncated backpropagation)。initial_state 从 0 开始,并在每轮计算中进行重置。因此,我们仍然能在一个特定的批次中从之前的 seq_len 序列里保存表示的某些类型。这么做的原因在于,在字符这种级别上,一个极小的序列并不能够学习到足够多的表示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 def generate_batch (FLAGS, raw_data) : raw_X, raw_y = raw_data data_length = len(raw_X) num_batches = FLAGS.DATA_SIZE // FLAGS.BATCH_SIZE data_X = np.zeros([num_batches, FLAGS.BATCH_SIZE], dtype=np.int32) data_y = np.zeros([num_batches, FLAGS.BATCH_SIZE], dtype=np.int32) for i in range(num_batches): data_X[i, :] = raw_X[FLAGS.BATCH_SIZE * i: FLAGS.BATCH_SIZE * (i+1 )] data_y[i, :] = raw_y[FLAGS.BATCH_SIZE * i: FLAGS.BATCH_SIZE * (i+1 )] feed_size = FLAGS.BATCH_SIZE // FLAGS.SEQ_LEN for i in range(feed_size): X = data_X[:, i * FLAGS.SEQ_LEN:(i+1 ) * FLAGS.SEQ_LEN] y = data_y[:, i * FLAGS.SEQ_LEN:(i+1 ) * FLAGS.SEQ_LEN] yield (X, y)
下面是使用我们自己的权重的代码。rnn_cell 函数用来接收来自前一个单元的输入和状态,从而生成 RNN 的输出,同时也是下一个单元的输入状态。下一个函数 rnn_logits 使用权重将我们的 RNN 输出进行转换,从而通过 softmax 生成 logits 概率并用于分类。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def rnn_cell (FLAGS, rnn_input, state) : with tf.variable_scope('rnn_cell' , reuse=True ): W_input = tf.get_variable('W_input' , [FLAGS.NUM_CLASSES, FLAGS.NUM_HIDDEN_UNITS]) W_hidden = tf.get_variable('W_hidden' , [FLAGS.NUM_HIDDEN_UNITS, FLAGS.NUM_HIDDEN_UNITS]) b_hidden = tf.get_variable('b_hidden' , [FLAGS.NUM_HIDDEN_UNITS], initializer=tf.constant_initializer(0.0 )) return tf.tanh(tf.matmul(rnn_input, W_input) + tf.matmul(state, W_hidden) + b_hidden) def rnn_logits (FLAGS, rnn_output) : with tf.variable_scope('softmax' , reuse=True ): W_softmax = tf.get_variable('W_softmax' , [FLAGS.NUM_HIDDEN_UNITS, FLAGS.NUM_CLASSES]) b_softmax = tf.get_variable('b_softmax' , [FLAGS.NUM_CLASSES], initializer=tf.constant_initializer(0.0 )) return tf.matmul(rnn_output, W_softmax) + b_softmax
我们将输入和独热编码在 RNN 的批处理中进行 reshape 操作。然后,我们就可以使用 rnn_cell、rnn_logits 和 softmax 来运行我们的 RNN 从而预测下一个 token 了。你可以看到,我们生成的状态与我们在这个简单实现中的 RNN 输出是一致的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 class model (object) : def __init__ (self, FLAGS) : self.X = tf.placeholder(tf.int32, [None , None ], name='input_placeholder' ) self.y = tf.placeholder(tf.int32, [None , None ], name='labels_placeholder' ) self.initial_state = tf.zeros([FLAGS.NUM_BATCHES, FLAGS.NUM_HIDDEN_UNITS]) X_one_hot = tf.one_hot(self.X, FLAGS.NUM_CLASSES) rnn_inputs = [tf.squeeze(i, squeeze_dims=[1 ]) \ for i in tf.split(1 , FLAGS.SEQ_LEN, X_one_hot)] with tf.variable_scope('rnn_cell' ): W_input = tf.get_variable('W_input' , [FLAGS.NUM_CLASSES, FLAGS.NUM_HIDDEN_UNITS]) W_hidden = tf.get_variable('W_hidden' , [FLAGS.NUM_HIDDEN_UNITS, FLAGS.NUM_HIDDEN_UNITS]) b_hidden = tf.get_variable('b_hidden' , [FLAGS.NUM_HIDDEN_UNITS], initializer=tf.constant_initializer(0.0 )) state = self.initial_state rnn_outputs = [] for rnn_input in rnn_inputs: state = rnn_cell(FLAGS, rnn_input, state) rnn_outputs.append(state) self.final_state = rnn_outputs[-1 ] with tf.variable_scope('softmax' ): W_softmax = tf.get_variable('W_softmax' , [FLAGS.NUM_HIDDEN_UNITS, FLAGS.NUM_CLASSES]) b_softmax = tf.get_variable('b_softmax' , [FLAGS.NUM_CLASSES], initializer=tf.constant_initializer(0.0 )) logits = [rnn_logits(FLAGS, rnn_output) for rnn_output in rnn_outputs] self.predictions = [tf.nn.softmax(logit) for logit in logits] y_as_list = [tf.squeeze(i, squeeze_dims=[1 ]) \ for i in tf.split(1 , FLAGS.SEQ_LEN, self.y)] losses = [tf.nn.sparse_softmax_cross_entropy_with_logits(logit, label) \ for logit, label in zip(logits, y_as_list)] self.total_loss = tf.reduce_mean(losses) self.train_step = tf.train.AdagradOptimizer( FLAGS.LEARNING_RATE).minimize(self.total_loss)
我们偶尔也会从模型中进行采样。对于采样而言,可以选择使用 logits 概率中的最大值,或者在选择的类别中引入 temperature 参数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 def sample (self, FLAGS, sampling_type=1 ) : initial_state = tf.zeros([1 ,FLAGS.NUM_HIDDEN_UNITS]) predictions = [] state = initial_state for char in FLAGS.START_TOKEN: idx = FLAGS.char_to_idx[char] idx_one_hot = tf.one_hot(idx, FLAGS.NUM_CLASSES) rnn_input = tf.reshape(idx_one_hot, [1 , 65 ]) state = rnn_cell(FLAGS, rnn_input, state) logit = rnn_logits(FLAGS, state) prediction = tf.argmax(tf.nn.softmax(logit), 1 )[0 ] predictions.append(prediction.eval()) for token_num in range(FLAGS.PREDICTION_LENGTH-1 ): idx_one_hot = tf.one_hot(prediction, FLAGS.NUM_CLASSES) rnn_input = tf.reshape(idx_one_hot, [1 , 65 ]) state = rnn_cell(FLAGS, rnn_input, state) logit = rnn_logits(FLAGS, state) next_char_dist = logit/FLAGS.TEMPERATURE next_char_dist = tf.exp(next_char_dist) next_char_dist /= tf.reduce_sum(next_char_dist) dist = next_char_dist.eval() if sampling_type == 0 : prediction = tf.argmax(tf.nn.softmax( next_char_dist), 1 )[0 ].eval() elif sampling_type == 1 : prediction = FLAGS.NUM_CLASSES - 1 point = random.random() weight = 0.0 for index in range(0 , FLAGS.NUM_CLASSES): weight += dist[0 ][index] if weight >= point: prediction = index break else : raise ValueError("Pick a valid sampling_type!" ) predictions.append(prediction) return predictions
我们还需要看看如何向数据流中传递 initial_state 参数。为了避免梯度消失的出现,每次处理完一个序列后,它和 final_state 都会被更新。注意,我们将零初始状态作为起始状态,然后在将这个状态传递给随后的序列,并将前一个序列的 final_state 作为新的输入状态。
1 2 3 4 5 6 state = np.zeros([FLAGS.NUM_BATCHES, FLAGS.NUM_HIDDEN_UNITS]) for step, (input_X, input_y) in enumerate(epoch): predictions, total_loss, state, _= model.step(sess, input_X, input_y, state) training_losses.append(total_loss)
五、使用 TF RNN 实现 与上面不同的是,在下面这个实现中,我们将使用 TensorFlow 的 NN 工具来创建 RNN 抽象类。在使用这些类之前,理解这些类的输入内容、内部操作及输出结果是很重要的。由于我们仍然是使用基本的 rnn_cell,因此我们将使用截断误差反向传播,但是如果使用 GRU 或 LSTM,就没有必要了。其实,只需将整个数据分割成 batch_size,然后处理整个序列就可以了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 def rnn_cell (FLAGS) : if FLAGS.MODEL == 'rnn' : rnn_cell_type = tf.nn.rnn_cell.BasicRNNCell elif FLAGS.MODEL == 'gru' : rnn_cell_type = tf.nn.rnn_cell.GRUCell elif FLAGS.MODEL == 'lstm' : rnn_cell_type = tf.nn.rnn_cell.BasicLSTMCell else : raise Exception("Choose a valid RNN unit type." ) single_cell = rnn_cell_type(FLAGS.NUM_HIDDEN_UNITS) single_cell = tf.nn.rnn_cell.DropoutWrapper(single_cell, output_keep_prob=1 -FLAGS.DROPOUT) stacked_cell = tf.nn.rnn_cell.MultiRNNCell([single_cell] * FLAGS.NUM_LAYERS) return stacked_cell
上面的代码创建的是我们特定的 RNN 结构。我们可以从许多不同的 RNN 单元类型中进行选择,但是在这里你可以看到三个最常见的类型(BasicRNN、GRU 和 LSTM)。我们用一定数量的隐藏单元来创建每个 RNN 单元。然后,我们可以在每个单元层之后之后添加一个 Dropout 层来进行正则化处理。最后,我们可以通过复制 single_cell 来实现堆叠的 RNN 结构。注意,state_is_tuple=True 条件被附加到了 single_cell 和 stacked_cell 里。这保证了在给定序列的每个输入之后返回一个包含状态的元组。如果使用 LSTM 单元,上述语句为真;否则无视。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 def rnn_inputs (FLAGS, input_data) : with tf.variable_scope('rnn_inputs' , reuse=True ): W_input = tf.get_variable("W_input" , [FLAGS.NUM_CLASSES, FLAGS.NUM_HIDDEN_UNITS]) embeddings = tf.nn.embedding_lookup(W_input, input_data) return embeddings def rnn_softmax (FLAGS, outputs) : with tf.variable_scope('rnn_softmax' , reuse=True ): W_softmax = tf.get_variable("W_softmax" , [FLAGS.NUM_HIDDEN_UNITS, FLAGS.NUM_CLASSES]) b_softmax = tf.get_variable("b_softmax" , [FLAGS.NUM_CLASSES]) logits = tf.matmul(outputs, W_softmax) + b_softmax return logits
这里的 rnn_inputs 函数与原生 TensorFlow 版本的实现由一些不同。正如你所看到的,我们不再需要 reshape 输入。这是因为 tf.nn.dynamic_rnn 会帮我们处理来自 RNN 的 output 和 state。这是一种效率非常高的 RNN 抽象,它还要求输入的数据不被预先 reshape,因此我们所有全部内容都是嵌入的。rnn_softmax 类提供的 logits 功能和前面所实现内容的完全一样。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 class model (object) : def __init__ (self, FLAGS) : ''' 数据占位符''' self.input_data = tf.placeholder(tf.int32, [None , None ]) self.targets = tf.placeholder(tf.int32, [None , None ]) ''' RNN 单元 ''' self.stacked_cell = rnn_cell(FLAGS) self.initial_state = self.stacked_cell.zero_state( FLAGS.NUM_BATCHES, tf.float32) ''' RNN 输入 ''' with tf.variable_scope('rnn_inputs' ): W_input = tf.get_variable("W_input" , [FLAGS.NUM_CLASSES, FLAGS.NUM_HIDDEN_UNITS]) inputs = rnn_inputs(FLAGS, self.input_data) ''' RNN 输出 ''' outputs, state = tf.nn.dynamic_rnn(cell=self.stacked_cell, inputs=inputs, initial_state=self.initial_state) outputs = tf.reshape(tf.concat(1 , outputs), [-1 , FLAGS.NUM_HIDDEN_UNITS]) ''' 处理 RNN 输出 ''' with tf.variable_scope('rnn_softmax' ): W_softmax = tf.get_variable("W_softmax" , [FLAGS.NUM_HIDDEN_UNITS, FLAGS.NUM_CLASSES]) b_softmax = tf.get_variable("b_softmax" , [FLAGS.NUM_CLASSES]) self.logits = rnn_softmax(FLAGS, outputs) self.probabilities = tf.nn.softmax(self.logits) ''' Loss ''' y_as_list = tf.reshape(self.targets, [-1 ]) self.loss = tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits( self.logits, y_as_list)) self.final_state = state ''' 优化 ''' self.lr = tf.Variable(0.0 , trainable=False ) trainable_vars = tf.trainable_variables() grads, _ = tf.clip_by_global_norm(tf.gradients(self.loss, trainable_vars), FLAGS.GRAD_CLIP) optimizer = tf.train.AdamOptimizer(self.lr) self.train_optimizer = optimizer.apply_gradients( zip(grads, trainable_vars)) self.global_step = tf.Variable(0 , trainable=False ) self.saver = tf.train.Saver(tf.all_variables())
还要注意的是,我们不会手动的在嵌入之前对输入 token 进行独热编码,这是因为rnn_inputs 函数里的 tf.nn.embedding_lookup 会自动帮我们完成。
为了生成输出,我们使用了 tf.nn.dynamic_rnn ,其输出结果为每个输入的输出以及返回状态(即包含上一次每个输入批次的状态的元组)。最后,我们将输出进行了 reshape ,从而得到 logits 概率并用于与 targets 进行比较。
注意到 self.initial_state 由 stacked_cell.zero_state 初始化,我们只需要指定的 batch_size 就够了。对于这里的 NUM_BATCHES 请查看前面的张量形状一节中的说明。有一种替代方法可以不包含初始状态,dynamic_rnn() 会自行处理,我们所需要做的就是指定数据类型(即dtype = tf.float32 等)。可惜我们并不能这样做,因为我们要把序列的 final_state 作为了下一个序列的 initial_state 。你可能还会注意到,尽管 self.initial_state 不是占位符,我们还是把前一次 final_state 传给了新的 initial_state。当然,我们可以通过重新定义 step() 里的 self.initial_state 来输入自己的初始值。不管怎样,一旦用到 input_feeds ,我们就需要计算 output_feed,而如果没有用到,那么就会跳回使用重载之前的值(也就是 stacked_cell.zero_state)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def step (self, sess, batch_X, batch_y, initial_state=None) : if initial_state == None : input_feed = {self.input_data: batch_X, self.targets: batch_y} else : input_feed = {self.input_data: batch_X, self.targets: batch_y, self.initial_state: initial_state} output_feed = [self.loss, self.final_state, self.logits, self.train_optimizer] outputs = sess.run(output_feed, input_feed) return outputs[0 ], outputs[1 ], outputs[2 ], outputs[3 ]
结果 我们来看看结果。这绝不是一种惊天动地的创造,但我确实是用了 temperature 而不是 argmax 进行生成。因此,我们可以看到生成结果里包含很多新奇的创意,但同时错误也很多(包括语法、拼写、排序等)。我只让网络训练了 10 轮,但已经开始看到单词和句子结构了,甚至还能看到每个角色的表演台词(数据集是莎士比亚的作品)。为了获得不错的结果,可以让它通宵在 GPU 上进行训练。
看到这,估计连莎士比亚都要给跪了。
更新 :我对典型输入、输出和状态张量的形状有很多疑问。
输入 :[num_batches, seq_len, num_classes]输出 :[num_batches, seq_len, num_hidden_units] (每个状态的全部输出)状态 :[num_batches, num_hidden_units] (上一次状态的输出)
在下一篇文章中,我们将处理变长序列,展示文本分类的具体实现。