在第一篇文章中，我们看到了如何使用 TensorFlow 实现一个简单的 RNN 架构。现在我们将使用这些组件并将其应用到文本分类中去。主要的区别在于，我们不会像 CHAR-RNN 模型那样输入固定长度的序列，而是使用长度不同的序列。

文本分类

这个任务的数据集选用了来自 Cornell 大学的语句情绪极性数据集，它包含了 5331 个正面和负面情绪的句子。这是一个非常小的数据集，但足够用来演示如何使用循环神经网络进行文本分类了。

预处理步骤

  1. 清洗句子并切分成一个个 token；
  2. 将句子转换为数值 token；
  3. 保存每个句子的序列长。

如上图所示，我们希望在计算完成时立即对句子的情绪做出预测。引入额外的填充符会带来过多噪声，这样的话你模型的性能就会不太好。注意：我们填充序列的唯一原因是因为需要以固定大小的批量输入进 RNN。下面你会看到，使用动态 RNN 还能避免在序列完成后的不必要计算。

模型

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
class model(object):

    def __init__(self, FLAGS):

        # 占位符
        self.inputs_X = tf.placeholder(tf.int32,
            shape=[None, None], name='inputs_X')
        self.targets_y = tf.placeholder(tf.float32,
            shape=[None, None], name='targets_y')
        self.dropout = tf.placeholder(tf.float32)

        # RNN 单元
        stacked_cell = rnn_cell(FLAGS, self.dropout)

        # RNN 输入
        with tf.variable_scope('rnn_inputs'):
            W_input = tf.get_variable("W_input",
                [FLAGS.en_vocab_size, FLAGS.num_hidden_units])

        inputs = rnn_inputs(FLAGS, self.inputs_X)
        #initial_state = stacked_cell.zero_state(FLAGS.batch_size, tf.float32)

        # RNN 输出
        seq_lens = length(self.inputs_X)
        all_outputs, state = tf.nn.dynamic_rnn(cell=stacked_cell, inputs=inputs,
            sequence_length=seq_lens, dtype=tf.float32)

        # 由于使用了 seq_len[0]，state 自动包含了上一次的对应输出
        # 因为 state 是一个带有张量的元组
        outputs = state[0]

        # 处理 RNN 输出
        with tf.variable_scope('rnn_softmax'):
            W_softmax = tf.get_variable("W_softmax",
                [FLAGS.num_hidden_units, FLAGS.num_classes])
            b_softmax = tf.get_variable("b_softmax", [FLAGS.num_classes])

        # Logits
        logits = rnn_softmax(FLAGS, outputs)
        probabilities = tf.nn.softmax(logits)
        self.accuracy = tf.equal(tf.argmax(
            self.targets_y,1), tf.argmax(logits,1))

        # 损失函数
        self.loss = tf.reduce_mean(
            tf.nn.sigmoid_cross_entropy_with_logits(logits, self.targets_y))

        # 优化
        self.lr = tf.Variable(0.0, trainable=False)
        trainable_vars = tf.trainable_variables()
        # 使用梯度截断来避免梯度消失和梯度爆炸
        grads, _ = tf.clip_by_global_norm(
            tf.gradients(self.loss, trainable_vars), FLAGS.max_gradient_norm)
        optimizer = tf.train.AdamOptimizer(self.lr)
        self.train_optimizer = optimizer.apply_gradients(
            zip(grads, trainable_vars))

        # 下面是用于采样的值
        # (在每个单词后生成情绪)

        # 取所有输出作为第一个输入序列
        # (由于采样，只需一个输入序列)
        sampling_outputs = all_outputs[0]

        # Logits
        sampling_logits = rnn_softmax(FLAGS, sampling_outputs)
        self.sampling_probabilities = tf.nn.softmax(sampling_logits)

        # 保存模型的组件
        self.global_step = tf.Variable(0, trainable=False)
        self.saver = tf.train.Saver(tf.all_variables())

    def step(self, sess, batch_X, batch_y=None, dropout=0.0,
        forward_only=True, sampling=False):

        input_feed = {self.inputs_X: batch_X,
                      self.targets_y: batch_y,
                      self.dropout: dropout}

        if forward_only:
            if not sampling:
                output_feed = [self.loss,
                               self.accuracy]
            elif sampling:
                input_feed = {self.inputs_X: batch_X,
                              self.dropout: dropout}
                output_feed = [self.sampling_probabilities]
        else: # 训练
            output_feed = [self.train_optimizer,
                           self.loss,
                           self.accuracy]

        outputs = sess.run(output_feed, input_feed)

        if forward_only:
            if not sampling:
                return outputs[0], outputs[1]
            elif sampling:
                return outputs[0]
        else: # 训练
            return outputs[0], outputs[1], outputs[2]

上面的代码就是我们的模型代码，它在训练的过程中使用了输入的文本。注意：为了清楚起见，我们决定将批量数据的大小保存在我们的输入和目标占位符中，但是我们应该让它们独立于一个特定的批量大小之外。由于这个特定的批量大小依赖于 batch_size，如果我们这么做，那么我们就还得输入一个 initial_state。我们通过嵌入他们来为每个数据序列来输入 token。实践策略表明，我们在输入文本上使用 skip-gram 模型预训练嵌入权重能够取得更好的性能。

在此模型中，我们再次使用 dynamic_rnn，但是这次我们提供了sequence_length 参数的值，它是一个包含每个序列长度的列表。这样，我们就可以避免在输入序列的最后一个词之后进行的不必要的计算。length 函数就用来获取这个列表的长度，如下所示。当然，我们也可以在外面计算seq_len，再通过占位符进行传递。

1
2
3
4
5
def length(data):
	relevant = tf.sign(tf.abs(data))
	length = tf.reduce_sum(relevant, reduction_indices=1)
	length = tf.cast(length, tf.int32)
	return length

由于我们填充符 token 为 0，因此可以使用每个 token 的 sign 性质来确定它是否是一个填充符 token。如果输入大于 0，则 tf.sign 为 1；如果输入为 0，则为 tf.sign 为 0。这样，我们可以逐步通过列索引来获得 sign 值为正的 token 数量。至此，我们可以将这个长度提供给 dynamic_rnn 了。

注意：我们可以很容易地在外部计算 seq_lens，并将其作为占位符进行传参。这样我们就不用依赖于 PAD_ID = 0 这个性质了。

一旦我们从 RNN 拿到了所有的输出和最终状态，我们就会希望分离对应输出。对于每个输入来说，将具有不同的对应输出，因为每个输入长度不一定不相同。由于我们将 seq_len 传给了 dynamic_rnn，而 state 又是最后一个对应输出，我们可以通过查看 state 来找到对应输出。注意，我们必须取 state[0]，因为返回的 state 是一个张量的元组。

其他需要注意的事情：我并没有使用 initial_state，而是直接给 dynamic_rnn 设置 dtype。此外，dropout 将根据 forward_only 与否，作为参数传递给 step()。

推断

总的来说，除了单个句子的预测外，我还想为具有一堆样本句子整体情绪进行预测。我希望看到的是，每个单词都被 RNN 读取后，将之前的单词分值保存在内存中，从而查看预测分值是怎样变化的。举例如下（值越接近 0 表明越靠近负面情绪）：

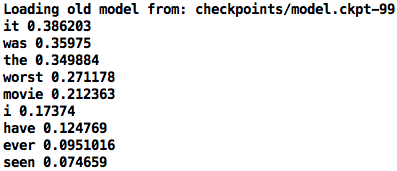
注意：这是一个非常简单的模型，其数据集非常有限。主要目的只是为了阐明它是如何搭建以及如何运行的。为了获得更好的性能，请尝试使用数据量更大的数据集，并考虑具体的网络架构，比如 Attention 模型、Concept-Aware 词嵌入以及隐喻（symbolization to name）等等。

损失屏蔽（这里不需要）

最后，我们来计算 cost。你可能会注意到我们没有做任何损失屏蔽（loss masking）处理，因为我们分离了对应输出，仅用于计算损失函数。然而，对于其他诸如机器翻译的任务来说，我们的输出很有可能还来自填充符 token。我们不想考虑这些输出，因为传递了 seq_lens 参数的 dynamic_rnn 将返回 0。下面这个例子比较简单，只用来说明这个实现大概是怎么回事；我们这里再一次使用了填充符 token 为 0 的性质：

1
2
3
4
5
# 向量化 logits 和目标
targets = tf.reshape(targets, [-1]) # 将张量 targets 转为向量
losses = tf.nn.sparse_softmax_cross_entropy_with_logits(logits, targets)
mask = tf.sign.(tf.to_float(targets)) # targets 为 0 则输出为 0, target < 0 则输出为 -1, 否则 为 1
masked_losses = mask*losses # 填充符所在位置的贡献为 0

首先我们要将 logits 和 targets 向量化。为了使 logits 向量化，一个比较好的办法是将 dynamic_rnn 的输出向量化为 [-1，num_hidden_units] 的形状，然后乘以 softmax 权重 [num_hidden_units，num_classes]。通过损失屏蔽操作，就可以消除填充符所在位置贡献的损失。

张量形状变化的参考

原始未处理过的文本 X 形状为 [N,] 而 y 的形状为 [N, C]，其中 C 是输出类别的数量（这些是手动完成的，但我们需要使用独热编码来处理多类情况）。

然后 X 被转化为 token 并进行填充，变成了 [N, ]。我们还需要传递形状为 [N,] 的 seq_len 参数，包含每个句子的长度。

现在 X、seq_len 和 y 通过这个模型首先嵌入为 [NXD]，其中 D 是嵌入维度。X 便从 [N, ] 转换为了 [N, , D]。回想一下，X 在这里有一个中间表示，它被独热编码为了 [N, , ]。但我们并不需要这么做，因为我们只需要使用对应词的索引，然后从词嵌入权重中取值就可以了。

我们需要将这个嵌入后的 X 传递给 dynamic_rnn 并返回 all_outputs （[N, , D]）以及 state（[1, N, D]）。由于我们输入了 seq_lens，对于我们而言它就是最后一个对应的状态。从维度的角度来说，你可以看到， all_outputs 就是来自 RNN 的对于每个句子中的每个词的全部输出结果。然而，state 仅仅只是每个句子的最后一个对应输出。

现在我们要输入 softmax 权重，但在此之前，我们需要通过取第一个索引（state[0]）来把状态从 [1,N,D] 转换为[N,D]。如此便可以通过与 softmax 权重 [D,C] 的点积，来得到形状为 [N,C] 的输出。其中，我们做指数级 softmax 运算，然后进行正则化，最终结合形状为 [N,C] 的 target_y 来计算损失函数。

注意：如果你使用了基本的 RNN 或者 GRU，从 dynamic_rnn 返回的 all_outputs 和 state 的形状是一样的。但是如果使用 LSTM 的话，all_outputs 的形状就是 [N, , D] 而 state 的形状为 [1, 2, N, D]。