机器学习算法在视觉领域和自然语言处理领域已经带来了很大的改变。但是音乐呢？近几年，音乐信息检索领域一直在飞速发展。这篇文章写的是NLP的一些技术是如何移植到音乐领域的。探寻了一种使用流行的 NLP 技术 word2vec 来表示复调音乐的方法。让我们来探究一下这是如何做到的……
Word2vec
词嵌入模型使我们能够通过有意义的方式表示词汇，这样机器学习模型就可以更容易地处理它们。这些词嵌入模型让我们可以用包含语义的向量来表示词汇。Word2vec 是一个流行的词向量嵌入模型，由 Mikolov 等人于 2013 年开发，它能够以一种十分有效的方式创建语义向量空间。
Word2vec 的本质是一个简单的单层神经网络，它有两种构造方式：1）使用连续词袋模型（CBOW）；或 2）使用 skip-gram 结构。这两种结构都非常高效，并且可以相对快速地进行训练。在本研究中，我们使用的是 skip-gram 模型，因为 Mikolov 等人在 2013 年的工作中提到，这个方法对于较小的数据集更加高效。Skip-gram 结构使用当前词 w_t 作为输入（输入层），并尝试预测在窗口范围内与之前后相邻的词（输出层）：
由于一些在网上流传的图片，人们对于 skip-gram 结构的样子存在一些疑惑。网络的输出层并不包含多个单词，而是由上下文窗口中的一个单词组成的。那么它如何才能表示整个上下文窗口呢？当训练网络时，我们实际会使用抽样对，它由输入单词和一个上下文窗口中的随机单词组成。
这种类型的网络的传统训练目标包含一个用 softmax 函数来计算 𝑝(𝑤_{𝑡+𝑖}|𝑤_𝑡) 的过程，而它的梯度计算代价是十分大的。幸运的是，诸如噪音对比估计（Gutmann 和 Hyvärine 于 2012 发表论文）和负采样（Mikolov 等人于 2013 年发表论文）等技术为此提供了一个解决方案。我们用负采样基本地定义一个新的目标：最大化真实单词的概率并最小化噪声样本的概率。一个简单的二元逻辑回归可以用来分类真实单词和噪声样本。
当 word2vec 模型训练好了，隐藏层上的权重基本上就可以表示习得的、多维的嵌入结果。
用音乐作为单词？
音乐和语言是存在内在联系的。它们都由遵从一些语法规则的一系列有序事件组成。更重要的是，它们都会创造出预期。想象一下，如果我说：“我要去比萨店买一个……”。这句话就生成了一个明确的预期……比萨。现在想象我给你哼一段生日快乐的旋律，但是我在最后一个音符前停下了……所以就像一句话一样，旋律生成预期，这些预期可以通过脑电波测量到，比如大脑中的事件相关电位 N400（Besson 和 Schön 于 2002 年发表论文）。
考虑语到语言和单词的相似性，让我们看看流行的语言模型是否也可以用来对音乐做有意义的表达。为了将一个 midi 文件转换为“语言”，我们在音乐中定义“切片”（相当于语言中的单词）。我们数据库中的每个曲目都被分割成了等时长的、不重叠的、长度为一个节拍的切片。一个节拍的时长可以由 MIDI toolbox 得到，且在每个曲目中可以是不同的。对于每一个切片，我们都会记录一个包含所有音名的列表，也就是没有八度信息的音高。
下图展示了一个怎样从 Chopin’s Mazurka Op. 67 №4 的第一小节中确定切片的例子。这里一节拍的长度是四分音符。
Word2vec 学习调性 —— 音乐的语义分布假设
在语言模型中，语义分布假设是词向量嵌入背后的理论基础之一。它表述为“出现在同一上下文中的单词趋向于含有同样的语义”。翻译到向量空间，这意味着这些单词会在几何关系上彼此接近。让我们看看 word2vec 模型是否在音乐上也学习到了类似的表示。
数据集
Chuan 等人使用的 MIDI 数据集 包含了 8 种不同音乐类型（从古典到金属）。在总共 130,000 个音乐作品中，基于类型标签，我们只选择了其中的 23,178 个。这些曲目包含了 4,076 个唯一的切片。
超参数
模型的训练只使用了出现最多的 500 个切片（即单词），并使用一个伪造单词来替代所有其他的情况。当包含的单词含有更多的信息（出现次数）时，这个过程提高了模型的准确性。其他的超参数包括学习率（设为 0.1），skip 窗口大小（设为 4），训练步数（设为 1,000,000）和嵌入维度（设为 256）。
和弦
为了评估音乐切片的语义是否被模型捕获，让我们来看看和弦。
在切片词库中，所有包括三和弦的切片都会被识别出来。然后用罗马数字标注这些切片的音级（就像我们在乐理中经常做的那样）。比如，在C调中，C和弦为 I，而G和弦表示为 V。之后我们会使用余弦距离来计算在嵌入中不同音级的和弦之间有多远。
在 n 维空间中，两个非零向量 A 和 B 的余弦距离 Ds(A, B) 计算如下：
D𝑐(A,B)=1-cos(𝜃)=1-D𝑠(A,B)
其中 𝜃 是 A 和 B 的夹角，Ds 是余弦相似度：
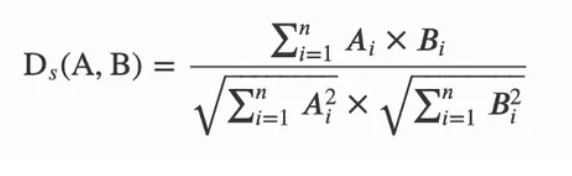
从乐理视角看，和弦 I 和 V 之间的“音调距离”应该比和弦 I 和 III 之间的小。下图展示了C大三和弦与其他和弦之间的距离。
从三和弦 I 到 V、IV 和 vi 的距离相对比较小！这与他们在乐理中被认为的“音调接近”是一致的，同时也表示 word2vec 模型的确学习到了切片之间有意义的关系。
在 word2vec 空间下，和弦之间的余弦距离似乎反映出了乐理中和弦的功能作用！
调
通过观察巴赫的《平均律钢琴曲集》（WTC）的 24 首前奏曲，其中包括了全部的 24 个调（大调和小调），我们可以研究新的嵌入空间是否捕获到了调的信息。
为了扩充数据集，每个曲子都被转换为其他每一种大调或小调（基于原调），这样每个曲子都会有 12 个版本。每个调的切片都会被映射到预先训练好的向量空间里，并使用 k-means 聚类，这样我们就能得到一些中心点，把它们作为新数据集中的曲子。通过把这些曲子变调，我们可以保证这些中心点之间的余弦距离只会受到一个元素的影响：调。
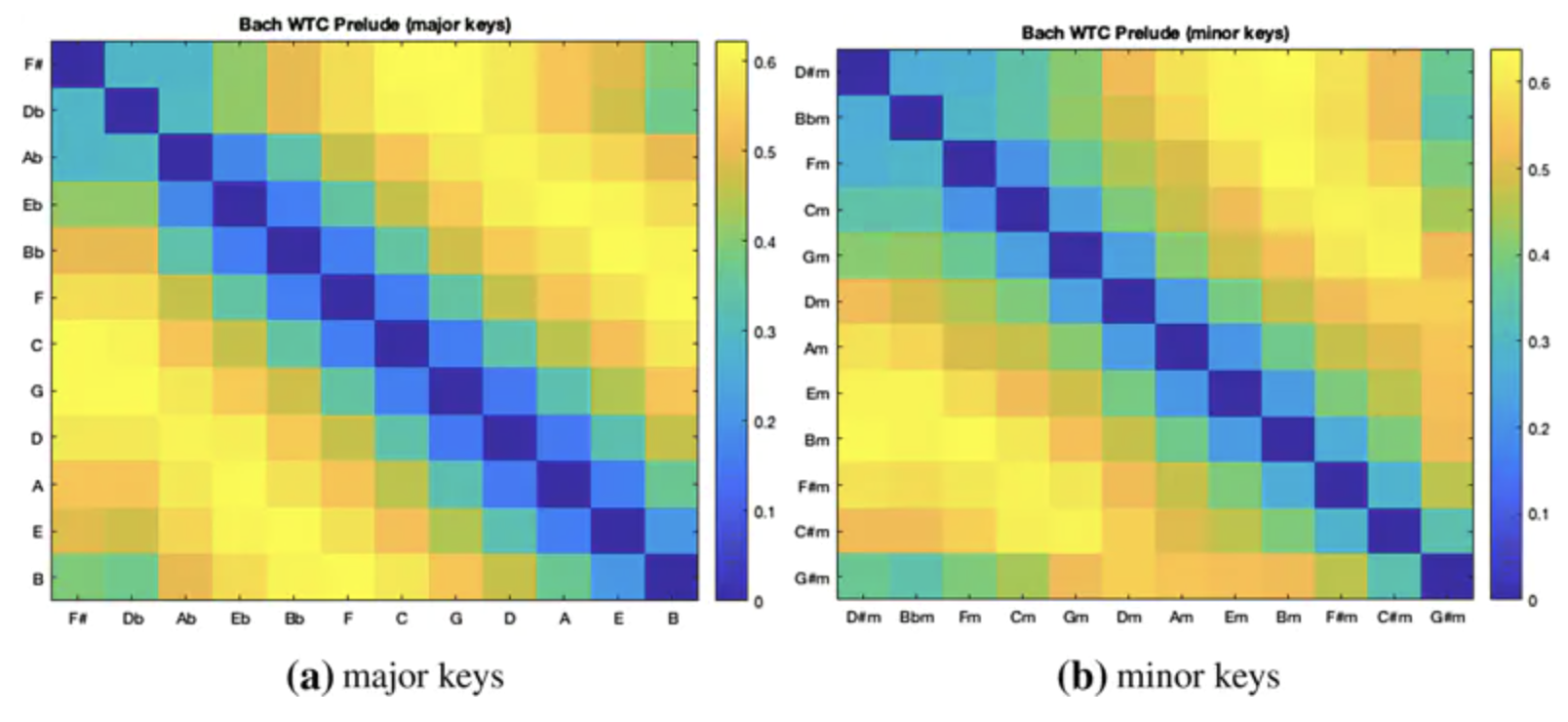
下图展示了不同调的中心点曲子之间的余弦距离结果。和预期的一样，差五度音程的调在音调上是接近的，它们被表示为对角线旁边较暗的区域。音调上较远的调（比如 F 和 F#）呈橙色，这验证了我们的假设，即 word2vec 空间反映了调之间的音调距离关系！
类推
这张图片
展示了 word2vec 的一个突出的特性，它可以在向量空间中找出类似于「国王 -> 皇后」和「男人 -> 女人」这样的转化关系（Mikolov 等人 于 2013 年发表论文）。这说明含义可以通过向量转化向前传递。那么对音乐来说是否也可行呢？
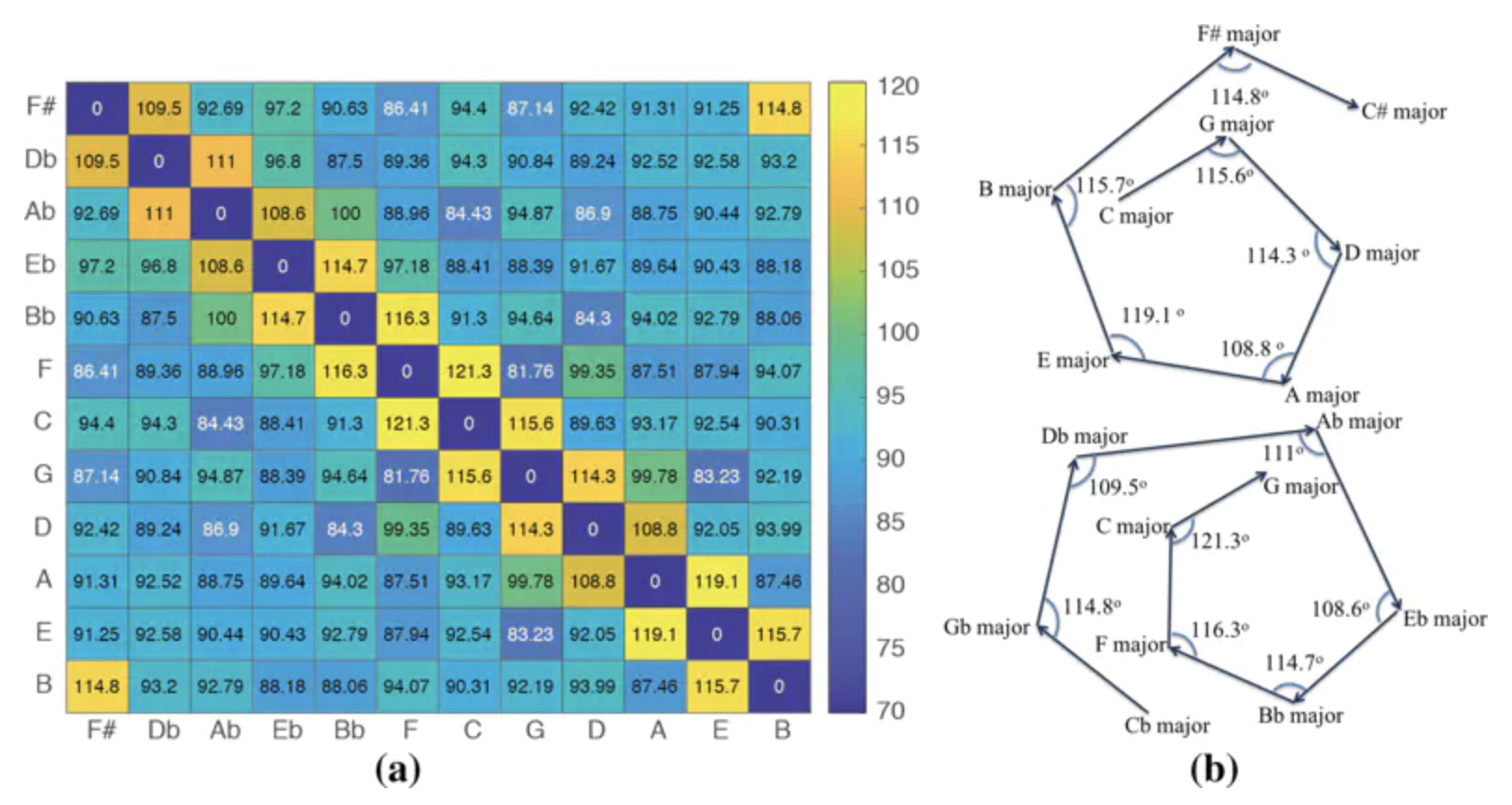
我们首先从多音切片中检测到一些和弦，并观察一对和弦向量，C大调到G大调（I-V）。可以发现，不同的 I-V 向量对之间的夹角都非常相似（如右图所示），甚至可以被想成一个多维的五度圈。这再一次证明了类推的概念可能也存在于音乐 word2vec 空间上，尽管要想发现更明确的例子还需要做更多的调查研究。
其它应用 —— 音乐生成？
Chuan 等人于 2018 年简要地研究了如何使用该模型替换音乐切片以形成新的音乐。他们表示这只是一个初步的实验，但是该系统可以作为一个表示方法而用于更复杂的系统，例如 LSTM。在论文中可以找到更多相关细节，但下图可以让你对其结果有一个初步的了解。
结论
Chuan、Agres 和 Herremans 于 2018 年创建了一种 word2vec 模型，这种模型可以捕捉到复调音乐的音调属性，而无需将实际的音符输入模型。文章给出了一些令人信服的证据，说明和弦与调的信息可以在新的嵌入中找到，所以可以这样回答标题中的问题：是的，我们能够使用 word2vec 表示复调音乐！现在，将这个表示方法嵌入到其他能够捕捉到音乐的时间信息的模型，这条道路也已经打开了。